التوزيع ذو الحدين للمتغيرات العشوائية وخصائصه. التوزيع ذو الحدين لمتغير عشوائي. دعونا نواصل حل المشاكل معا

يعد التوزيع ذو الحدين أحد أهم التوزيعات الاحتمالية للمتغير العشوائي المتغير بشكل منفصل. التوزيع ذو الحدين هو التوزيع الاحتمالي للرقم موقوع حدث ما أالخامس نملاحظات مستقلة بشكل متبادل. في كثير من الأحيان حدث أيسمى "نجاح" الملاحظة، والحدث المعاكس يسمى "الفشل"، ولكن هذه التسمية مشروطة للغاية.

شروط التوزيع ذات الحدين:

• في المجموع نفذت نالمحاكمات التي يقع فيها الحدث أقد يحدث أو لا يحدث؛
• حدث أفي كل تجربة يمكن أن يحدث بنفس الاحتمال ص;
• الاختبارات مستقلة بشكل متبادل.

احتمال أن في نحدث الاختبار أسوف يأتي بالضبط ميمكن حساب الأوقات باستخدام صيغة برنولي:

أين ص- احتمال وقوع حدث أ;

س = 1 - ص- احتمال وقوع الحدث المعاكس.

دعونا معرفة ذلك لماذا يرتبط التوزيع ذو الحدين بصيغة برنولي بالطريقة الموضحة أعلاه؟ . الحدث - عدد النجاحات في نوتنقسم الاختبارات إلى عدد من الخيارات، في كل منها يتم تحقيق النجاح مالاختبارات والفشل في ن - مالاختبارات. دعونا نفكر في أحد هذه الخيارات - ب1 . باستخدام قاعدة جمع الاحتمالات، نضرب احتمالات الأحداث المعاكسة:

,

وإذا دلنا س = 1 - ص، الذي - التي

.

أي خيار آخر فيه مالنجاح و ن - مالفشل. عدد هذه الخيارات يساوي عدد الطرق التي يمكن للمرء أن يفعلها نالحصول على اختبار منجاح.

مجموع كل الاحتمالات مأرقام حدوث الحدث أ(الأرقام من 0 إلى ن) يساوي واحد:

حيث يمثل كل حد حدًا في ذات الحدين لنيوتن. ولذلك، فإن التوزيع قيد النظر يسمى التوزيع ذي الحدين.

في الممارسة العملية، غالبا ما يكون من الضروري حساب الاحتمالات "ليس أكثر من مالنجاح في نالاختبارات" أو "على الأقل مالنجاح في نالاختبارات". يتم استخدام الصيغ التالية لهذا الغرض.

الوظيفة التكاملية، أي احتمالا F(م) مادا في نحدث رصدي ألن يأتي المزيد ممرة واحدة، يمكن حسابها باستخدام الصيغة:

في دورها احتمالا F(≥م) مادا في نحدث رصدي أسوف يأتي لا أقل ممرة واحدة، يتم حسابه بواسطة الصيغة:

في بعض الأحيان يكون من المناسب حساب احتمالية ذلك نحدث رصدي ألن يأتي المزيد ممرات، من خلال احتمال الحدث المعاكس:

.

تعتمد الصيغة التي سيتم استخدامها على أي منها يحتوي على مجموع يحتوي على عدد أقل من الحدود.

يتم حساب خصائص التوزيع ذي الحدين باستخدام الصيغ التالية .

القيمة المتوقعة: .

تشتت: .

الانحراف المعياري: .

التوزيع ذو الحدين والحسابات في MS Excel

احتمال ذو الحدين صن( م) وقيم الدالة التكاملية F(م) يمكن حسابها باستخدام الدالة MS Excel BINOM.DIST. تظهر نافذة الحساب المقابل أدناه (انقر بزر الماوس الأيسر للتكبير).

يتطلب منك MS Excel إدخال البيانات التالية:

• عدد النجاحات
• عدد الاختبارات
• احتمالية النجاح
• تكامل - القيمة المنطقية: 0 - إذا كنت بحاجة إلى حساب الاحتمال صن( م) و 1 - إذا كان الاحتمال F(م).

مثال 1.قام مدير الشركة بتلخيص المعلومات حول عدد الكاميرات المباعة خلال آخر 100 يوم. يلخص الجدول المعلومات ويحسب احتمالات بيع عدد معين من الكاميرات يوميًا.

وينتهي اليوم بالربح إذا تم بيع 13 كاميرا أو أكثر. احتمال أن يتم عمل اليوم بشكل مربح:

احتمال أن يعمل يوم بدون ربح:

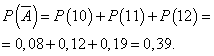
وليكن احتمال عمل يوم مع ربح ثابتًا ويساوي 0.61، ولا يعتمد عدد الكاميرات المباعة يوميًا على اليوم. ثم يمكننا استخدام التوزيع ذي الحدين، حيث يقع الحدث أ- اليوم سيعمل بالربح - بدون ربح.

احتمال أن يتم تحقيق الربح خلال الأيام الستة كلها:

.

نحصل على نفس النتيجة باستخدام وظيفة MS Excel BINOM.DIST (قيمة القيمة المتكاملة هي 0):

ص 6 (6 ) = BINOM.DIST(6; 6; 0.61; 0) = 0.052.

احتمالية أن يتم عمل 4 أيام أو أكثر من 6 أيام مع الربح:

أين ,

,

باستخدام دالة MS Excel BINOM.DIST، نحسب احتمالية إكمال ما لا يزيد عن 3 أيام من أصل 6 أيام مع تحقيق ربح (قيمة القيمة المتكاملة هي 1):

ص 6 (≤3 ) = BINOM.DIST(3; 6; 0.61; 1) = 0.435.

احتمالية أن يتم التعامل مع الأيام الستة كلها بخسائر:

,

يمكننا حساب نفس المؤشر باستخدام وظيفة MS Excel BINOM.DIST:

ص 6 (0 ) = BINOM.DIST(0; 6; 0.61; 0) = 0.0035.

حل المشكلة بنفسك ثم شاهد الحل

مثال 2.هناك كرتان أبيضتان و3 كرات سوداء في الجرة. يتم إخراج كرة من الجرة، ويتم ضبط اللون وإعادته. وتكرر المحاولة 5 مرات. عدد مرات ظهور الكرات البيضاء هو متغير عشوائي منفصل X، موزعة وفقا لقانون ذات الحدين. صياغة قانون توزيع المتغير العشوائي. تحديد الوضع والتوقع الرياضي والتشتت.

دعونا نواصل حل المشاكل معا

مثال 3.من خدمة البريد السريع ذهبنا إلى المواقع ن= 5 سعاة. من المحتمل أن يكون كل ساعي ص= 0.3، بغض النظر عن الآخرين، متأخر عن الكائن. المتغير العشوائي المنفصل X- عدد السعاة المتأخرين. أنشئ سلسلة توزيع لهذا المتغير العشوائي. أوجد التوقع الرياضي والتباين والانحراف المعياري. أوجد احتمال تأخر اثنين على الأقل من السعاة عن تسليم العناصر.

مرحبًا! نحن نعرف بالفعل ما هو التوزيع الاحتمالي. يمكن أن تكون منفصلة أو مستمرة، وتعلمنا أنها تسمى دالة الكثافة الاحتمالية. الآن دعونا نفحص اثنين من التوزيعات الأكثر شيوعا. لنفترض أن لدي عملة معدنية، عملة عادلة، وسأقوم بقلبها 5 مرات. سأقوم أيضًا بتعريف المتغير العشوائي X، الذي يُشار إليه بالحرف الكبير X، وسيكون مساويًا لعدد الرؤوس في 5 رميات. ربما أملك 5 عملات معدنية، وسأقلبها كلها مرة واحدة وأحسب عدد الرؤوس التي سأحصل عليها. أو يمكنني الحصول على عملة معدنية واحدة، ويمكنني أن أقلبها 5 مرات وأحسب عدد المرات التي حصلت فيها على صورة. لا يهم حقا. ولكن لنفترض أن لدي عملة معدنية واحدة وسأقوم بقلبها 5 مرات. عندها لن يكون لدينا أي شك. إذن هذا هو تعريف المتغير العشوائي الخاص بي. كما نعلم، المتغير العشوائي يختلف قليلاً عن المتغير العادي، فهو أشبه بالدالة. أنه يعين بعض المعنى للتجربة. وهذا المتغير العشوائي بسيط للغاية. نحن ببساطة نحسب عدد المرات التي ظهرت فيها "الرؤوس" بعد 5 رميات - وهذا هو المتغير العشوائي X. دعونا نفكر في احتمالات القيم المختلفة في حالتنا؟ إذًا، ما هو احتمال أن يكون X (الحرف الكبير X) هو 0؟ أولئك. ما هو احتمال أنه بعد 5 رميات لن يكون هناك رؤوس؟ حسنًا، هذا هو في الأساس نفس احتمال الحصول على الصور فقط (هذا صحيح، نظرة عامة قصيرة على نظرية الاحتمالات). يجب أن تحصل على ذيول فقط. ما هو احتمال كل من هذه الرؤوس؟ هذا هو 1/2. أولئك. ينبغي أن يكون هذا 1/2 ضرب 1/2 و1/2 و1/2 و1/2 مرة أخرى. أولئك. (١/٢)⁵. 1⁵=1، القسمة على 2⁵، أي. في 32. منطقي تماما. لذا... سأكرر قليلاً ما تناولناه في نظرية الاحتمالات. هذا مهم لفهم المكان الذي نتحرك فيه الآن وكيف يتم في الواقع تشكيل التوزيع الاحتمالي المنفصل. إذًا، ما هو احتمال أن نحصل على "رؤوس" مرة واحدة بالضبط؟ حسنًا، قد تظهر الرؤوس عند الرمية الأولى. أولئك. يمكن أن تكون: "رؤوس"، "ذيول"، "ذيول"، "ذيول"، "ذيول". أو يمكن أن تظهر الرؤوس في الرمية الثانية. أولئك. يمكن أن يكون هناك مزيج مثل هذا: "ذيول"، "رؤوس"، "ذيول"، "ذيول"، "ذيول" وما إلى ذلك. يمكن أن يظهر "رأس" واحد بعد أي من الرميات الخمس. ما هو احتمال كل من هذه الحالات؟ احتمال الحصول على الرؤوس هو 1/2. ثم يتم ضرب احتمال الحصول على رؤوس يساوي 1/2 في 1/2، في 1/2، في 1/2. أولئك. احتمال كل من هذه المواقف هو 1/32. نفس احتمال الموقف حيث X = 0. بشكل أساسي، احتمالية أي ترتيب معين للرؤوس والذيول ستكون 1/32. لذا فإن احتمال حدوث ذلك هو 1/32. واحتمال ذلك هو 1/32. وتحدث مثل هذه المواقف بسبب احتمال سقوط "الرؤوس" في أي من الرميات الخمس. ولذلك فإن احتمال ظهور "رأس" واحد بالضبط هو 5*1/32، أي. 5/32. منطقي تماما. الآن أصبحت الأمور مثيرة للاهتمام. ما هو الاحتمال... (سأكتب كل مثال بلون مختلف)... ما هو احتمال أن يكون المتغير العشوائي الخاص بي يساوي 2؟ أولئك. رميت قطعة نقود 5 مرات، فما احتمال سقوطها على الصورة مرتين بالضبط؟ هذا أكثر إثارة للاهتمام، أليس كذلك؟ ما هي المجموعات الممكنة؟ يمكن أن تكون رؤوسًا، رؤوسًا، ذيولًا، ذيولًا، ذيولًا. ويمكن أيضًا أن تكون "رؤوس"، "ذيول"، "رؤوس"، "ذيول"، "ذيول". وإذا كنت تعتقد أن هذين "النسرين" يمكن أن يكونا في أماكن مختلفة في المجموعة، فقد تشعر بالارتباك قليلاً. لم يعد من الممكن التفكير في المواضع بالطريقة التي فعلناها هنا أعلاه. على الرغم من... أنك تستطيع ذلك، إلا أنك تخاطر بالارتباك. يجب أن تفهم شيئا واحدا. لكل من هذه المجموعات الاحتمال هو 1/32. ½*½*½*½*½. أولئك. احتمال كل من هذه المجموعات هو 1/32. وعلينا أن نفكر في عدد هذه المجموعات التي تلبي حالتنا (2 "رأس")؟ أولئك. في الأساس، عليك أن تتخيل أن هناك 5 رميات للعملة المعدنية، وعليك اختيار اثنتين منها حيث تظهر "الصورة". دعونا نتخيل أن رمياتنا الخمس مجتمعة في دائرة، ونتخيل أيضًا أن لدينا كرسيين فقط. ونقول: "حسنًا، من منكم سيجلس على كراسي النسر هذه؟ أولئك. من منكم سيكون "النسر"؟ ونحن لسنا مهتمين بالترتيب الذي يجلسون فيه. أضرب هذا المثال، آملا أن يكون أكثر وضوحا بالنسبة لك. وقد ترغب في مشاهدة بعض دروس الاحتمالات حول هذا الموضوع عندما أتحدث عن ذات الحدين لنيوتن. لأنني سأتحدث عن كل هذا بمزيد من التفصيل. ولكن إذا كنت تفكر بهذه الطريقة، سوف تفهم ما هو معامل ذات الحدين. لأنه إذا كنت تفكر بهذه الطريقة: حسنًا، لدي 5 رميات، أي رمية ستحصل على "الرؤوس" الأولى؟ حسنًا، إليك 5 احتمالات سيؤدي القذف فيها إلى ظهور "الرؤوس" الأولى. كم عدد الفرص المتاحة للنسر الثاني؟ حسنًا، الرمية الأولى التي استخدمناها بالفعل أزالت احتمالية واحدة للحصول على رؤوس. أولئك. موضع رأس واحد في المجموعة مشغول بالفعل بإحدى الرميات. الآن تبقى 4 رميات، مما يعني أن "الرؤوس" الثانية يمكن أن تسقط على إحدى الرميات الأربع. ولقد رأيت ذلك، هنا. اخترت أن يكون هناك رأس في الرمية الأولى، وافترضت أن إحدى الرميات الأربع المتبقية ستؤدي أيضًا إلى ظهور الرأس. لذلك هناك 4 احتمالات فقط هنا. كل ما أقوله هو أنه بالنسبة للرؤوس الأولى، لديك 5 أوضاع مختلفة يمكن أن تهبط عليها. وللثاني لم يتبق سوى 4 وظائف. فكر في الأمر. عندما نحسب مثل هذا، يتم أخذ الترتيب في الاعتبار. لكن بالنسبة لنا الآن لا يهم الترتيب الذي تسقط به "الرؤوس" و"الذيول". لا نقول أنها رؤوس 1 أو رؤوس 2. وفي كلتا الحالتين هو مجرد رؤوس. قد نخمن أن هذا هو الرؤوس 1 وهذا هو الرؤوس 2. أو يمكن أن يكون العكس: قد يكون هذا "النسر" الثاني، وهذا يمكن أن يكون "الأول". وأنا أقول هذا لأنه من المهم أن نفهم مكان استخدام المواضع ومكان استخدام المجموعات. نحن لسنا مهتمين بالاتساق. لذا، في الواقع، هناك طريقتان فقط يمكن أن يحدث بها هذا الحدث. لذا نقسم هذا على 2. وكما سترون لاحقًا، هناك 2! طرق أصل هذا الحدث لدينا. إذا كان هناك 3 رؤوس، فسيكون هناك 3 هنا! وسأوضح لك السبب. لذلك، سيكون هذا مساويًا لـ... 5*4=20 ومقسمًا على 2 - تحصل على 10. إذن هناك 10 مجموعات مختلفة من أصل 32 سيكون لديك فيها بالتأكيد رأسان. إذًا، 10*(1/32) يساوي 10/32، فماذا يساوي ذلك؟ 5/16. سأكتبها بدلالة معامل ذي الحدين. هذه هي القيمة هنا في الأعلى. إذا فكرت في الأمر، هذا هو نفس 5!، مقسومًا على... ماذا يعني هذا 5*4؟ 5! – هذا هو 5*4*3*2*1. أولئك. إذا كنت بحاجة فقط إلى 5*4 هنا، فيمكنني تقسيم 5 لهذا! بحلول 3! وهذا يساوي 5*4*3*2*1 مقسومًا على 3*2*1. وبقي 5*4 فقط. إذن، هذا هو نفس هذا البسط. وبعد ذلك، لأن نحن لسنا مهتمين بالتسلسل، نحتاج هنا إلى 2. في الواقع، 2!. اضرب في 1/32. سيكون هذا هو احتمال حصولنا على رأسين بالضبط. ما هو احتمال أن نحصل على صورة 3 مرات بالضبط؟ أولئك. احتمال أن X = 3. لذلك، وبنفس المنطق، قد تحدث الحالة الأولى للرؤوس في رمية واحدة من أصل 5. قد تحدث الحالة الثانية للرؤوس في إحدى الرميات الأربع المتبقية. والحالة الثالثة من "الرؤوس" قد تحدث في إحدى الرميات الثلاث المتبقية. ما عدد الطرق المختلفة المتوفرة لترتيب 3 رميات؟ بشكل عام، ما عدد الطرق المتاحة لوضع ثلاثة أشياء في أماكنها؟ هذا 3! ويمكنك اكتشاف ذلك، أو قد ترغب في مراجعة تلك الدروس التي شرحت فيها ذلك بمزيد من التفصيل. ولكن إذا كنت، على سبيل المثال، تأخذ الحروف A وB وC، فهناك إجمالي 6 طرق يمكنك من خلالها ترتيبها. يمكنك التفكير في هذه كحالات للرؤوس. يمكن أن يكون هناك ACB، CAB هنا. يمكن أن يكون BAC، BCA، و... ما هو الخيار الأخير الذي لم أذكره؟ CBA. هناك 6 طرق لترتيب 3 أشياء مختلفة. نقسم على 6 لأننا لا نريد إعادة حساب هذه الطرق الست المختلفة لأننا نعاملها على قدم المساواة. نحن هنا لسنا مهتمين بأي رمية ستؤدي إلى ظهور الرؤوس. 5*4*3... يمكن إعادة كتابتها بالشكل 5!/2!. وتقسيمها على 3 آخرين!. هذا هو. 3! يساوي 3*2*1. يتم تقليل الثلاثات. وهذا يصبح يساوي 2. وهذا يصبح يساوي 1. ومرة ​​أخرى، 5*2، أي. يساوي 10. كل موقف لديه احتمال 1/32، لذا فهذا يساوي 5/16 مرة أخرى. وهذا مثير للاهتمام. احتمال حصولك على 3 رؤوس يساوي احتمال حصولك على رأسين. والسبب في ذلك... حسنًا، هناك العديد من الأسباب التي أدت إلى حدوث ذلك. ولكن إذا فكرت في الأمر، فإن احتمال الحصول على 3 صور هو نفس احتمال الحصول على 2 كتابة. واحتمال الحصول على 3 رؤوس يجب أن يكون هو نفسه احتمال الحصول على رأسين. ومن الجيد أن تعمل القيم بهذه الطريقة. بخير. ما هو احتمال أن X = 4؟ يمكننا استخدام نفس الصيغة التي استخدمناها من قبل. يمكن أن يكون 5*4*3*2. إذًا، نكتب هنا 5*4*3*2... بكم طريقة مختلفة لترتيب 4 أشياء؟ هذا هو 4!. 4! - هذا، في الواقع، هذا الجزء هنا. هذا هو 4*3*2*1. لذلك، يتم تقليل هذا، ويتبقى 5. بعد ذلك، كل مجموعة لديها احتمال 1/32. أولئك. وهذا يساوي 5/32. ولاحظ مرة أخرى أن احتمال الحصول على الصورة 4 مرات يساوي احتمال الحصول على الصورة مرة واحدة. وهذا منطقي، لأن... 4 رؤوس هو نفس الحصول على ذيل واحد. تقول: حسنًا، في أي رمية سيظهر هذا "الذيول"؟ نعم، هناك 5 مجموعات مختلفة لهذا الغرض. وكل واحد منهم لديه احتمال 1/32. وأخيرًا، ما هو احتمال أن يكون X = 5؟ أولئك. تظهر الرؤوس 5 مرات متتالية. يجب أن يكون مثل هذا: "النسر"، "النسر"، "النسر"، "النسر"، "النسر". كل رأس لديه احتمال 1/2. اضربهم واحصل على 1/32. يمكنك الذهاب بطريقة أخرى. إذا كان هناك 32 طريقة يمكنك من خلالها الحصول على صور وذيول في هذه التجارب، فهذه مجرد واحدة من تلك الطرق. هنا كانت هناك 5 طرق من أصل 32. هنا - 10 من 32. ومع ذلك، قمنا بإجراء الحسابات، والآن نحن على استعداد لرسم التوزيع الاحتمالي. لكن وقتي انتهى. اسمحوا لي أن أواصل في الدرس التالي. وإذا كنت في مزاج جيد، فربما يمكنك الرسم قبل مشاهدة الدرس التالي؟ اراك قريبا!

في هذه المقالة والمشاركات القليلة القادمة سنلقي نظرة على النماذج الرياضية للأحداث العشوائية. نموذج رياضيهو تعبير رياضي يمثل متغير عشوائي. بالنسبة للمتغيرات العشوائية المنفصلة، ​​يُعرف هذا التعبير الرياضي بوظيفة التوزيع.

إذا كانت المشكلة تسمح لك بكتابة تعبير رياضي يمثل متغيرًا عشوائيًا بشكل صريح، فيمكنك حساب الاحتمال الدقيق لأي من قيمه. في هذه الحالة، يمكنك حساب وإدراج جميع قيم دالة التوزيع. يتم العثور على مجموعة متنوعة من توزيعات المتغيرات العشوائية في التطبيقات التجارية والاجتماعية والطبية. واحدة من التوزيعات الأكثر فائدة هي ذات الحدين.

توزيع ثنائيتستخدم لمحاكاة المواقف التي تتميز بالميزات التالية.

• تتكون العينة من عدد محدد من العناصر ن، يمثل نتائج اختبار معين.
• ينتمي كل عنصر عينة إلى إحدى الفئتين المتعارضتين اللتين تستنفدان مساحة العينة بأكملها. عادة ما تسمى هاتين الفئتين بالنجاح والفشل.
• احتمالية النجاح رثابت. ولذلك فإن احتمال الفشل هو 1 – ص.
• إن نتيجة أي تجربة (أي النجاح أو الفشل) لا تعتمد على نتيجة تجربة أخرى. ولضمان استقلالية النتائج، يتم عادة الحصول على عناصر العينة باستخدام طريقتين مختلفتين. يتم سحب كل عنصر في العينة بشكل عشوائي من مجتمع لا نهائي بدون انعكاس أو من مجتمع محدود مع انعكاس.

قم بتنزيل المذكرة بالتنسيق أو بالأمثلة بالتنسيق

يستخدم التوزيع ذو الحدين لتقدير عدد النجاحات في عينة تتكون من نالملاحظات. لنأخذ الطلب كمثال. لتقديم الطلب، يمكن لعملاء شركة Saxon استخدام النموذج الإلكتروني التفاعلي وإرساله إلى الشركة. يقوم نظام المعلومات بعد ذلك بالتحقق من وجود أخطاء أو معلومات غير كاملة أو غير صحيحة في الطلبات. يتم وضع علامة على أي طلب معني وإدراجه في تقرير الاستثناء اليومي. تشير البيانات التي جمعتها الشركة إلى أن احتمال الأخطاء في الطلبات هو 0.1. ترغب إحدى الشركات في معرفة احتمال العثور على عدد معين من الطلبات الخاطئة في عينة معينة. على سبيل المثال، لنفترض أن العملاء قاموا بملء أربعة نماذج إلكترونية. ما هو احتمال أن تكون جميع الأوامر خالية من الأخطاء؟ كيف تحسب هذا الاحتمال؟ بالنجاح سنفهم خطأً عند ملء النموذج، وكل النتائج الأخرى ستعتبر فاشلة. تذكر أننا مهتمون بعدد الطلبات الخاطئة في عينة معينة.

ما هي النتائج التي يمكن أن نلاحظها؟ إذا كانت العينة مكونة من أربعة أوامر، فقد يكون واحد أو اثنان أو ثلاثة أو الأربعة جميعها غير صحيح، وقد تكون جميعها صحيحة. هل يمكن للمتغير العشوائي الذي يصف عدد النماذج المكتملة بشكل غير صحيح أن يأخذ أي قيمة أخرى؟ وهذا غير ممكن لأن عدد النماذج غير الصحيحة لا يمكن أن يتجاوز حجم العينة نأو تكون سلبية. وبالتالي فإن المتغير العشوائي الذي يخضع لقانون التوزيع ذي الحدين يأخذ القيم من 0 إلى ن.

لنفترض أنه في عينة مكونة من أربعة أوامر لوحظت النتائج التالية:

ما هو احتمال العثور على ثلاثة أوامر خاطئة في عينة مكونة من أربعة أوامر بالترتيب المحدد؟ بما أن الأبحاث الأولية أظهرت أن احتمال الخطأ عند ملء النموذج هو 0.10، فإن احتمالات النتائج المذكورة أعلاه يتم حسابها على النحو التالي:

وبما أن النتائج لا تعتمد على بعضها البعض، فإن احتمال التسلسل المحدد للنتائج يساوي: p*p*(1–p)*p = 0.1*0.1*0.9*0.1 = 0.0009. إذا كنت بحاجة إلى حساب عدد الاختيارات X نالعناصر، يجب عليك استخدام الصيغة المركبة (1):

حيث ن! = ن * (ن –1) * (ن – 2) * … * 2 * 1 - مضروب الرقم ن، و 0! = 1 و 1! = 1 حسب التعريف.

غالبًا ما يُشار إلى هذا التعبير باسم . وبالتالي، إذا كانت n = 4 وX = 3، فإن عدد التسلسلات المكونة من ثلاثة عناصر مستخرجة من عينة بحجم 4 يتم تحديدها بالصيغة التالية:

وعليه يتم حساب احتمال اكتشاف ثلاثة أوامر خاطئة على النحو التالي:

(عدد التسلسلات الممكنة) *
(احتمال تسلسل معين) = 4 * 0.0009 = 0.0036

وبالمثل، يمكنك حساب احتمال أن يكون هناك واحد أو اثنين من الأوامر الخاطئة من بين أربعة أوامر، بالإضافة إلى احتمال أن تكون جميع الأوامر خاطئة أو كلها صحيحة. ولكن مع زيادة حجم العينة نيصبح تحديد احتمالية تسلسل معين من النتائج أكثر صعوبة. في هذه الحالة، يجب عليك تطبيق النموذج الرياضي المناسب الذي يصف التوزيع ذي الحدين لعدد الاختيارات Xكائنات من مجموعة تحتوي على نعناصر.

توزيع ثنائي

أين ف (س)- احتمالا Xالنجاح لحجم عينة معين نواحتمالية النجاح ر, X = 0, 1, … ن.

يرجى ملاحظة أن الصيغة (2) هي إضفاء الطابع الرسمي على الاستنتاجات البديهية. قيمة عشوائية X، الذي يخضع للتوزيع ذي الحدين، يمكنه أن يأخذ أي قيمة عددية في النطاق من 0 إلى ن. عمل رX(1 - ع)ن – Xيمثل احتمال تسلسل معين يتكون من Xالنجاح في حجم عينة يساوي ن. تحدد القيمة عدد المجموعات المحتملة التي تتكون من Xالنجاح في نالاختبارات. لذلك، لعدد معين من الاختبارات نواحتمالية النجاح راحتمال تسلسل يتكون من Xالنجاح، على قدم المساواة

P(X) = (عدد التسلسلات الممكنة) * (احتمال تسلسل معين) =

دعونا نفكر في أمثلة توضح تطبيق الصيغة (2).

1. لنفترض أن احتمال ملء النموذج بشكل غير صحيح هو 0.1. ما هو احتمال أن تكون هناك ثلاث نماذج غير صحيحة من بين أربعة نماذج مكتملة؟ وباستخدام الصيغة (2) نجد أن احتمال اكتشاف ثلاثة أوامر خاطئة في عينة مكونة من أربعة أوامر يساوي

2. لنفترض أن احتمال ملء النموذج بشكل غير صحيح هو 0.1. ما هو احتمال أن تكون ثلاث نماذج على الأقل غير صحيحة من بين أربعة نماذج مكتملة؟ كما هو موضح في المثال السابق، فإن احتمال أن تكون هناك ثلاثة نماذج غير صحيحة من بين أربعة نماذج مكتملة هو 0.0036. لحساب احتمال أن تكون ثلاثة نماذج على الأقل غير صحيحة من بين أربعة نماذج مكتملة، يتعين عليك إضافة احتمال أن تكون ثلاثة نماذج غير صحيحة من بين أربعة نماذج مكتملة واحتمال أن تكون جميع النماذج غير صحيحة من بين النماذج الأربعة المكتملة. احتمال الحدث الثاني هو

وبالتالي، فإن احتمال أن تكون هناك ثلاثة نماذج غير صحيحة من بين أربعة نماذج مكتملة يساوي

ف(X > 3) = ف(X = 3) + ف(X = 4) = 0.0036 + 0.0001 = 0.0037

3. لنفترض أن احتمال ملء النموذج بشكل غير صحيح هو 0.1. ما هو احتمال أن يكون من بين أربعة نماذج مكتملة أقل من ثلاثة نماذج غير صحيحة؟ احتمالية هذا الحدث

ف(س< 3) = P(X = 0) + P(X = 1) + P(X = 2)

باستخدام الصيغة (2)، نحسب كل من هذه الاحتمالات:

ولذلك، ف (X< 3) = 0,6561 + 0,2916 + 0,0486 = 0,9963.

الاحتمال P(X< 3) можно вычислить иначе. Для этого воспользуемся тем, что событие X < 3 является дополнительным по отношению к событию Х>3. ثم ف(X< 3) = 1 – Р(Х> 3) = 1 – 0,0037 = 0,9963.

كلما زاد حجم العينة نتصبح الحسابات المشابهة لتلك التي تم إجراؤها في المثال 3 صعبة. لتجنب هذه التعقيدات، يتم جدولة العديد من الاحتمالات ذات الحدين مسبقًا. وتظهر بعض هذه الاحتمالات في الشكل. 1. على سبيل المثال، للحصول على احتمال ذلك X= 2 في ن= 4 و ص= 0.1، عليك أن تستخرج من الجدول الرقم عند تقاطع الخط X= 2 والأعمدة ر = 0,1.

أرز. 1. احتمال ذو الحدين في ن = 4, X= 2 و ر = 0,1

يمكن حساب التوزيع ذي الحدين باستخدام دالة Excel =BINOM.DIST() (الشكل 2)، والتي تحتوي على 4 معلمات: عدد النجاحات - Xعدد الاختبارات (أو حجم العينة) - ناحتمال النجاح - ر، معامل أساسي، والتي تأخذ القيمة TRUE (في هذه الحالة، يتم حساب الاحتمال لا اقل Xالأحداث) أو FALSE (في هذه الحالة يتم حساب الاحتمال بالضبط Xالأحداث).

أرز. 2. معلمات الوظيفة =BINOM.DIST()

بالنسبة للأمثلة الثلاثة المذكورة أعلاه، تظهر الحسابات في الشكل. 3 (انظر أيضًا ملف Excel). يحتوي كل عمود على صيغة واحدة. توضح الأرقام الإجابات على أمثلة الرقم المقابل).

أرز. 3. حساب التوزيع ذي الحدين في برنامج Excel ل ن= 4 و ص = 0,1

خصائص التوزيع ذي الحدين

التوزيع ذو الحدين يعتمد على المعلمات نو ر. يمكن أن يكون التوزيع ذو الحدين متماثلًا أو غير متماثل. إذا كانت p = 0.05، يكون التوزيع ذو الحدين متماثلًا بغض النظر عن قيمة المعلمة ن. ومع ذلك، إذا كانت p ≠ 0.05، يصبح التوزيع منحرفًا. كلما اقتربت قيمة المعلمة رإلى 0.05 وكلما زاد حجم العينة ن، كلما كان عدم تناسق التوزيع أقل وضوحًا. وبالتالي، فإن توزيع عدد النماذج المكتملة بشكل غير صحيح ينحرف إلى اليمين بسبب ص= 0.1 (الشكل 4).

أرز. 4. رسم بياني للتوزيع ذي الحدين في ن= 4 و ص = 0,1

توقع التوزيع ذي الحدينيساوي منتج حجم العينة نعلى احتمال النجاح ر:

(3) م = ه(X) =n.p.

في المتوسط، مع وجود سلسلة طويلة بما فيه الكفاية من الاختبارات في عينة تتكون من أربعة أوامر، قد يكون هناك p = E(X) = 4 × 0.1 = 0.4 نماذج مكتملة بشكل غير صحيح.

الانحراف المعياري للتوزيع ذي الحدين

على سبيل المثال، الانحراف المعياري لعدد النماذج المكتملة بشكل غير صحيح في نظام المعلومات المحاسبية هو:

يتم استخدام مواد من كتاب ليفين وآخرين إحصائيات المديرين. – م: ويليامز، 2004. – ص. 307-313

- (التوزيع ذو الحدين) توزيع يسمح لك بحساب احتمال وقوع أي حدث عشوائي يتم الحصول عليه نتيجة لملاحظات عدد من الأحداث المستقلة، إذا كان احتمال وقوع مكوناتها الأولية ... ... القاموس الاقتصادي

- (توزيع برنولي) التوزيع الاحتمالي لعدد تكرارات حدث معين أثناء التجارب المستقلة المتكررة، إذا كان احتمال وقوع هذا الحدث في كل تجربة يساوي p(0p1). الرقم بالضبط ؟ حوادث هذا الحدث هي ...... القاموس الموسوعي الكبير

توزيع ثنائي- - موضوعات الاتصالات، المفاهيم الأساسية EN التوزيع ذو الحدين ...

- (توزيع برنولي) التوزيع الاحتمالي لعدد تكرارات حدث معين خلال التجارب المستقلة المتكررة، إذا كان احتمال وقوع هذا الحدث في كل تجربة يساوي p (0≥p≥1). وهي عدد μ مرات حدوث هذا الحدث ... ... القاموس الموسوعي

توزيع ثنائي- 1.49. التوزيع ذو الحدين التوزيع الاحتمالي لمتغير عشوائي منفصل X، مع أخذ أي قيم صحيحة من 0 إلى n، مثل x = 0، 1، 2، ...، n والمعلمات n = 1، 2، ... و 0< p < 1, где Источник … كتاب مرجعي للقاموس لمصطلحات التوثيق المعياري والتقني

توزيع برنولي، التوزيع الاحتمالي للمتغير العشوائي X، بأخذ القيم الصحيحة مع الاحتمالات، على التوالي (معامل ذي الحدين؛ المعلمة p لـ B. r.، تسمى احتمال النتيجة الإيجابية، بأخذ القيم ... الموسوعة الرياضية

التوزيع الاحتمالي لعدد مرات حدوث حدث معين أثناء التجارب المستقلة المتكررة. إذا كان احتمال وقوع حدث خلال كل تجربة يساوي p، مع 0 ≥ p ≥ 1، فإن عدد μ مرات حدوث هذا الحدث لـ n مستقل... ... الموسوعة السوفيتية الكبرى

- (توزيع برنولي) التوزيع الاحتمالي لعدد تكرارات حدث معين خلال التجارب المستقلة المتكررة، إذا كان احتمال وقوع هذا الحدث في كل تجربة يساوي p (0)<или = p < или = 1). Именно, число м появлений … علم الطبيعة. القاموس الموسوعي

توزيع الاحتمالية ذات الحدين- (التوزيع ذو الحدين) التوزيع الذي يتم ملاحظته في الحالات التي تأخذ فيها نتيجة كل تجربة مستقلة (الملاحظة الإحصائية) إحدى القيمتين المحتملتين: النصر أو الهزيمة، الشمول أو الاستبعاد، زائد أو ... القاموس الاقتصادي والرياضي

التوزيع الاحتمالي ذو الحدين- التوزيع الذي يتم ملاحظته في الحالات التي تأخذ فيها نتيجة كل تجربة مستقلة (الملاحظة الإحصائية) إحدى القيمتين المحتملتين: النصر أو الهزيمة، الشمول أو الاستبعاد، زائد أو ناقص، 0 أو 1. أي... ... دليل المترجم الفني

كتب

• نظرية الاحتمالية والإحصاء الرياضي في المشاكل. أكثر من 360 مسألة وتمارين، د.أ.بورزيخ. يحتوي الدليل المقترح على مهام ذات مستويات مختلفة من التعقيد. ومع ذلك، فإن التركيز الرئيسي ينصب على المهام ذات التعقيد المتوسط. ويتم ذلك عمدا لتشجيع الطلاب على ...
• نظرية الاحتمالية والإحصاء الرياضي في المسائل أكثر من 360 مشكلة وتمرين، د.بورزيخ.الدليل المقترح يحتوي على مسائل بمستويات مختلفة من التعقيد. ومع ذلك، فإن التركيز الرئيسي ينصب على المهام ذات التعقيد المتوسط. ويتم ذلك عمدا لتشجيع الطلاب على ...

دعونا نفكر في التوزيع ذي الحدين، ونحسب توقعه الرياضي، وتباينه، ومنواله. باستخدام الدالة MS EXCEL BINOM.DIST()، سنقوم برسم رسوم بيانية لوظيفة التوزيع وكثافة الاحتمال. دعونا نقدر معلمة التوزيع p والتوقع الرياضي للتوزيع والانحراف المعياري. دعونا نفكر أيضًا في توزيع برنولي.

تعريف. دعهم يحدثون نالتجارب، التي يمكن أن يحدث في كل منها حدثان فقط: الحدث "النجاح" مع الاحتمال ص أو حدث "فشل" مع احتمالية س =1-ع (ما يسمى مخطط برنولي,برنوليالمحاكمات).

احتمال الاستلام بالضبط س النجاح في هذه ن الاختبارات تساوي:

عدد النجاحات في العينة س هو متغير عشوائي لديه توزيع ثنائي(إنجليزي) ذو الحدينتوزيع) صو ن – هي معلمات هذا التوزيع.

يرجى تذكر أن للاستخدام مخططات برنوليوبالمقابل توزيع ثنائي،يجب استيفاء الشروط التالية:

• يجب أن يكون لكل اختبار نتيجتين بالضبط، يُطلق عليهما تقليديًا "النجاح" و"الفشل".
• ويجب ألا تعتمد نتيجة كل اختبار على نتائج الاختبارات السابقة (استقلال الاختبار).
• احتمال النجاح ص يجب أن تكون ثابتة لجميع الاختبارات.

التوزيع ذو الحدين في MS EXCEL

في MS EXCEL، بدءًا من الإصدار 2010، لـ هناك وظيفة BINOM.DIST()، الاسم الإنجليزي هو BINOM.DIST()، والذي يسمح لك بحساب احتمال وجوده بالضبط X"النجاح" (أي. دالة الكثافة الاحتماليةع (خ)، انظر الصيغة أعلاه)، و دالة التوزيع التراكمي(احتمال أن يكون للعينة سأو "نجاحات" أقل، بما في ذلك 0).

قبل MS EXCEL 2010، كان لدى EXCEL وظيفة BINOMDIST()، والتي تسمح لك أيضًا بحساب وظيفة التوزيعو كثافة الاحتمالع (خ). تم ترك BINOMIST() في MS EXCEL 2010 من أجل التوافق.

يحتوي ملف المثال على الرسوم البيانية توزيع الكثافة الاحتماليةو .

توزيع ثنائيلديه التعيين ب (ن ; ص) .

ملحوظة: للبناء دالة التوزيع التراكميمخطط النوع المثالي جدول، ل كثافة التوزيع – الرسم البياني مع التجميع. لمزيد من المعلومات حول إنشاء المخططات، اقرأ المقالة الأنواع الأساسية للمخططات.

ملحوظة: لتسهيل كتابة الصيغ، تم إنشاء أسماء المعلمات في ملف المثال توزيع ثنائي: ن و ص.

يعرض ملف المثال حسابات احتمالية مختلفة باستخدام وظائف MS EXCEL:

وكما ترون في الصورة أعلاه، فمن المفترض أن:

• يحتوي المجتمع اللانهائي الذي تم أخذ العينة منه على 10% (أو 0.1) من العناصر الصالحة (المعلمة ص، وسيطة الوظيفة الثالثة = BINOM.DIST() )
• لحساب احتمال وجود في عينة مكونة من 10 عناصر (المعلمة ن، الوسيطة الثانية للدالة) سيكون هناك بالضبط 5 عناصر صالحة (الوسيطة الأولى)، تحتاج إلى كتابة الصيغة: =BINOM.DIST(5، 10، 0.1، خطأ)
• تم تعيين العنصر الأخير والرابع = FALSE، أي. يتم إرجاع قيمة الدالة كثافة التوزيع .

إذا كانت قيمة الوسيطة الرابعة = TRUE، فإن الدالة BINOM.DIST() ترجع القيمة دالة التوزيع التراكميأو ببساطة وظيفة التوزيع. في هذه الحالة، يمكنك حساب احتمال أن يكون عدد العناصر الجيدة في العينة من نطاق معين، على سبيل المثال، 2 أو أقل (بما في ذلك 0).

للقيام بذلك تحتاج إلى كتابة الصيغة: = BINOM.DIST(2; 10; 0.1; صحيح)

ملحوظة: بالنسبة لقيمة غير صحيحة لـ x، . على سبيل المثال، الصيغ التالية سوف ترجع نفس القيمة: =BINOM.DIST( 2 ; 10؛ 0.1; حقيقي)=BINOM.DIST( 2,9 ; 10؛ 0.1; حقيقي)

ملحوظة: في ملف المثال كثافة الاحتمالو وظيفة التوزيعيتم حسابها أيضًا باستخدام التعريف والوظيفة NUMBERCOMB() .

مؤشرات التوزيع

في ملف المثال في ورقة العمل مثالهناك صيغ لحساب بعض مؤشرات التوزيع:

• =n*p;
• (مربع الانحراف المعياري) = n*p*(1-p);
• = (ن+1)*ص;
• =(1-2*ع)*ROOT(n*p*(1-p)).

دعونا نشتق الصيغة توقع رياضيتوزيع ثنائياستخدام دائرة برنولي .

بحكم التعريف، المتغير العشوائي X في مخطط برنولي(متغير برنولي العشوائي). وظيفة التوزيع :

ويسمى هذا التوزيع توزيع برنولي .

ملحوظة : توزيع برنولي- حالة خاصة توزيع ثنائيمع المعلمة ن=1.

لنقم بإنشاء 3 مصفوفات تحتوي كل منها على 100 رقم مع احتمالات نجاح مختلفة: 0.1؛ 0.5 و 0.9. للقيام بذلك في النافذة توليد أرقام عشوائيةدعونا نضبط المعلمات التالية لكل احتمال p:

ملحوظة: إذا قمت بتعيين الخيار تشتت عشوائي (البذور عشوائي)، ثم يمكنك تحديد مجموعة عشوائية محددة من الأرقام التي تم إنشاؤها. على سبيل المثال، من خلال تعيين هذا الخيار = 25، يمكنك إنشاء نفس مجموعات الأرقام العشوائية على أجهزة كمبيوتر مختلفة (إذا كانت معلمات التوزيع الأخرى هي نفسها بالطبع). يمكن أن تأخذ قيمة الخيار قيمًا صحيحة من 1 إلى 32767. اسم الخيار تشتت عشوائيقد يكون مربكا. سيكون من الأفضل ترجمتها كما رقم الطلب مع أرقام عشوائية .

ونتيجة لذلك، سيكون لدينا 3 أعمدة مكونة من 100 رقم، والتي يمكننا على أساسها، على سبيل المثال، تقدير احتمالية النجاح صوفقا للصيغة: عدد النجاحات/100(سم. مثال على ورقة الملف GenerationBernoulli).

ملحوظة: ل توزيعات برنوليمع p=0.5 يمكنك استخدام الصيغة =RANDBETWEEN(0;1) التي تتوافق مع .

توليد أرقام عشوائية. توزيع ثنائي

لنفترض أن هناك 7 منتجات معيبة في العينة. وهذا يعني أنه "من المحتمل جداً" أن تكون نسبة المنتجات المعيبة قد تغيرت ص، وهي سمة من سمات عملية الإنتاج لدينا. على الرغم من أن مثل هذا الموقف "محتمل جدًا"، إلا أن هناك احتمالًا (خطر ألفا، خطأ من النوع 1، "إنذار كاذب") صظلت دون تغيير، وكان العدد المتزايد من المنتجات المعيبة بسبب أخذ العينات العشوائية.

كما يتبين من الشكل أدناه، 7 هو عدد المنتجات المعيبة المقبولة لعملية ذات قيمة p=0.21 بنفس القيمة ألفا. يوضح هذا أنه عند تجاوز قيمة العتبة للعناصر المعيبة في العينة، صوقد زاد "الأغلب". عبارة "على الأغلب" تعني أن هناك احتمال 10% فقط (100%-90%) أن يكون انحراف نسبة المنتجات المعيبة عن الحد الأدنى لأسباب عشوائية فقط.

وبالتالي، فإن تجاوز الحد الأدنى لعدد المنتجات المعيبة في العينة يمكن أن يكون بمثابة إشارة إلى أن العملية أصبحت مضطربة وبدأت في إنتاج المنتجات المستعملة. يانسبة أعلى من المنتجات المعيبة.

ملحوظة: قبل MS EXCEL 2010، كان لدى EXCEL وظيفة CRITBINOM()، والتي تعادل BINOM.INV(). تم ترك CRITBINOM() في MS EXCEL 2010 والإصدارات الأحدث من أجل التوافق.

علاقة التوزيع ذي الحدين بالتوزيعات الأخرى

إذا كانت المعلمة نتوزيع ثنائييميل إلى اللانهاية، و صيميل إلى 0، ثم في هذه الحالة توزيع ثنائييمكن تقريبها. يمكننا صياغة الشروط عند التقريب توزيع السميعمل بشكل جيد:

• ص(الأقل صو اكثر نكلما كان التقريب أكثر دقة)؛
• ص >0,9 (معتبرا أن س =1- ص، يجب إجراء الحسابات في هذه الحالة من خلال س(أ Xيحتاج إلى استبداله ن - س). ولذلك، أقل سو اكثر نكلما كان التقريب أدق).

عند 0.110 توزيع ثنائييمكن تقريبها.

وبدورها، توزيع ثنائيقد يكون بمثابة تقريب جيد عندما يكون حجم السكان N التوزيع الهندسي الزائدأكبر بكثير من حجم العينة n (أي N>>n أو n/N). يمكنك قراءة المزيد عن العلاقة بين التوزيعات المذكورة أعلاه في المقالة. وترد أيضًا أمثلة على التقريب هناك، وشروط متى يكون ممكن وبأي دقة وأوضح.

نصيحة: يمكنك أن تقرأ عن توزيعات MS EXCEL الأخرى في المقالة.