تعريف.دع الدالة y = f (x) تُعرّف عند النقطة x0 وبعض المناطق المجاورة لها. يتم استدعاء الوظيفة y = f (x) مستمر عند النقطة x0، لو:

1. موجود
2. هذا الحد يساوي قيمة الدالة عند النقطة x0:

عند تحديد الحد ، تم التأكيد على أن f (x) قد لا يتم تعريفها عند النقطة x0 ، وإذا تم تعريفها في هذه المرحلة ، فإن قيمة f (x0) لا تشارك في تعريف الحد. عند تحديد الاستمرارية ، من الضروري وجود f (x0) ، ويجب أن تكون هذه القيمة مساوية لـ lim f (x).

تعريف.دع الدالة y = f (x) تُعرّف عند النقطة x0 وبعض المناطق المجاورة لها. تسمى الدالة f (x) متصلة عند النقطة x0 إذا كان هناك رقم موجب للجميع ε> 0 بحيث يكون لكل x من محيط النقطة x0 (أي | х-x0 |
هنا يؤخذ في الاعتبار أن قيمة الحد يجب أن تكون مساوية لـ f (x0) ، لذلك ، بالمقارنة مع تعريف الحد ، شرط ثقب δ-المجاورة 0
دعونا نعطي تعريفًا آخر (يعادل التعريفات السابقة) من حيث الزيادات. دلالة Δх = x - x0 ، ستسمى هذه القيمة زيادة الوسيطة. منذ x-> x0 ، ثم Δх-> 0 ، أي Δх - b.m (صغيرة بلا حدود). دلالة Δу = f (х) -f (x0) ، ستسمى هذه القيمة زيادة الوظيفة ، منذ | Δу | يجب أن يكون (لصغير بدرجة كافية | Δх |) أقل من رقم تعسفي ε> 0 ، ثم Δу أيضًا f.m. القيمة ، لذلك

تعريف.دع الدالة y = f (x) تُعرّف عند النقطة x0 وبعض المناطق المجاورة لها. تسمى الوظيفة f (x) مستمر عند النقطة x0، إذا كانت الزيادة المتناهية في الصغر للوسيطة تتوافق مع زيادة متناهية في الصغر للدالة.

تعريف.الدالة f (x) غير متصلة عند النقطة x0 ، يسمى متقطععند هذه النقطة.

تعريف.تسمى الوظيفة f (x) بشكل مستمر على مجموعة X إذا كانت متصلة في كل نقطة من هذه المجموعة.

نظرية استمرارية المجموع ، حاصل الضرب ، حاصل القسمة

نظرية المرور إلى النهاية تحت علامة الدالة المستمرة

نظرية الاستمرارية لتراكب الوظائف المستمرة

دع الوظيفة f (x) تُعرّف على فترة وتكون رتيبة في هذا الفاصل. عندئذٍ يمكن أن تحتوي f (x) على نقاط انقطاع فقط من النوع الأول في هذا المقطع.

نظرية القيمة المتوسطة.إذا كانت الدالة f (x) متصلة على مقطع ما وعند نقطتين a و b (a أقل من b) تأخذ قيمًا غير متساوية A = f (a) ≠ B = f (b) ، إذن لأي رقم C كذب بين A و B ، توجد نقطة c ∈ حيث تكون قيمة الوظيفة C: f (c) = C.

نظرية الحدود لوظيفة مستمرة في فترة.إذا كانت الدالة f (x) متصلة في فترة ما ، فيتم تقييدها على هذه الفترة.

نظرية الوصول إلى الحد الأدنى و القيم القصوى. إذا كانت الدالة f (x) متصلة على مقطع ما ، فإنها تصل إلى حدها السفلي والعلوي على هذا المقطع.

نظرية استمرارية الدالة العكسية.اجعل الدالة y = f (x) متصلة وتتزايد (تناقصًا) بشكل صارم في الفترة [а، b]. ثم يوجد في المقطع دالة عكسية x = g (y) ، والتي تتزايد أيضًا (تناقصًا) بشكل رتيب ومستمر.

استمرارية الوظيفة. نقاط كسر.

الثور يمشي ، يتأرجح ، يتنهد أثناء التنقل:
- أوه ، اللوحة تنتهي ، الآن سوف أسقط!

في هذا الدرس ، سنحلل مفهوم استمرارية الوظيفة ، وتصنيف نقاط الانقطاع ، والمشترك مهمة عملية التحقيق في وظيفة من أجل الاستمرارية. من عنوان الموضوع نفسه ، يخمن الكثيرون بشكل حدسي ما سيتم مناقشته ، ويعتقدون أن المادة بسيطة للغاية. هذا صحيح. لكنها مهام بسيطة يعاقب عليها في الغالب بسبب الإهمال ونهج سطحي لحلها. لذلك ، أوصي بأن تدرس المقالة بعناية وأن تلتقط كل التفاصيل الدقيقة والتقنيات.

ما الذي تريد أن تعرفه وتكون قادرًا على فعله؟ليس كثيرا. للحصول على تجربة تعليمية جيدة ، عليك أن تفهم ماذا حد الوظيفة. بالنسبة للقراء ذوي المستوى المنخفض من الإعداد ، يكفي فهم المقال حدود الوظائف. أمثلة الحلوالنظر المعنى الهندسيحد في الدليل الرسوم البيانية وخصائص الوظائف الابتدائية. من المستحسن أيضًا أن تتعرف على التحولات الهندسية للرسوم البيانية، لأن الممارسة في معظم الحالات تنطوي على بناء رسم. الاحتمالات متفائلة للجميع ، وحتى الغلاية الكاملة ستكون قادرة على التعامل مع المهمة بمفردها في الساعة أو الساعتين القادمتين!

استمرارية الوظيفة. نقاط التوقف وتصنيفها

مفهوم استمرارية الوظيفة

ضع في اعتبارك بعض الوظائف المستمرة على الخط الحقيقي بأكمله:

أو بعبارة أكثر إيجازًا ، فإن وظيفتنا مستمرة على (المجموعة أرقام حقيقية).

ما هو المعيار "الصغير" للاستمرارية؟ من الواضح أنه يمكن رسم الرسم البياني للدالة المستمرة دون رفع القلم الرصاص عن الورقة.

في هذه الحالة ، يجب التمييز بوضوح بين مفهومين بسيطين: نطاق الوظيفةو استمرارية الوظيفة. على العموم انه ليس نفس الشيئ. على سبيل المثال:

يتم تعريف هذه الوظيفة على خط الأعداد بالكامل ، أي لـ الجميعقيمة "x" لها قيمتها الخاصة "y". على وجه الخصوص ، إذا ، إذن. لاحظ أن النقطة الأخرى مثقوبة ، لأنه من خلال تعريف الوظيفة ، يجب أن تتطابق قيمة الوسيطة الشيء الوحيدقيمة الوظيفة. هكذا، اِختِصاصميزاتنا:.

لكن هذه الوظيفة ليست مستمرة!من الواضح أنها تتحمل في هذه المرحلة فجوة. المصطلح أيضًا واضح وواضح تمامًا ، في الواقع ، هنا يجب تمزيق قلم الرصاص من الورق على أي حال. بعد ذلك بقليل ، سننظر في تصنيف نقاط التوقف.

استمرارية دالة عند نقطة وفي فترة

في مسألة رياضية معينة ، يمكننا التحدث عن استمرارية دالة عند نقطة ، أو استمرارية دالة على فترة ، أو نصف فترة ، أو استمرارية دالة على مقطع. إنه، لا يوجد "استمرارية فقط"- يمكن أن تكون الوظيفة مستمرة في مكان ما. و "اللبنة" الأساسية لكل شيء آخر استمرارية الوظيفة في هذه النقطة .

تحدد نظرية التحليل الرياضي استمرارية الوظيفة عند نقطة ما بمساعدة أحياء "دلتا" و "إبسيلون" ، ولكن من الناحية العملية ، هناك تعريف آخر قيد الاستخدام ، والذي سنولي اهتمامًا وثيقًا له.

دعونا نتذكر أولا حدود من جانب واحدالذين اقتحموا حياتنا في الدرس الأول حول الرسوم البيانية للوظائف. ضع في اعتبارك الموقف اليومي:

إذا اقتربنا على طول المحور إلى النقطة غادر(السهم الأحمر) ، ثم القيم المقابلة من "الألعاب" سوف تسير على طول المحور إلى النقطة (سهم التوت). رياضيا حقيقة معينةثابت مع حد اليد اليسرى:

انتبه إلى الإدخال (يقرأ "x تميل إلى ka من اليسار"). يرمز "مضاف" "ناقص صفر" ، وهو ما يعني بشكل أساسي أننا نقترب من الرقم من الجانب الأيسر.

وبالمثل ، إذا اقتربت من النقطة "كا" على اليمين(السهم الأزرق) ، فإن "الألعاب" ستأتي بنفس القيمة ، ولكن على طول السهم الأخضر ، و حد اليد اليمنىسيتم تنسيقه على النحو التالي:

"الملحق" يرمز ، ويقرأ الإدخال على هذا النحو: "x تميل إلى ka من اليمين."

إذا كانت الحدود أحادية الجانب محدودة ومتساوية(كما في حالتنا): ، ثم نقول أن هناك حد عام. الأمر بسيط ، الحد الإجمالي هو "المعتاد" حد الوظيفةيساوي الرقم النهائي.

لاحظ أنه إذا لم يتم تحديد الوظيفة عند (ثقب النقطة السوداء في فرع الرسم البياني) ، فستظل الحسابات المدرجة صالحة. كما لوحظ مرارًا وتكرارًا ، ولا سيما في المقالة حول وظائف متناهية الصغر، التعبيرات تعني أن "x" قريب بلا حدوديقترب من النقطة ، بينما لا يهمما إذا كانت الوظيفة نفسها محددة في نقطة معينة أم لا. مثال جيدسيحدث في القسم التالي عند تحليل الوظيفة.

تعريف: دالة متصلة عند نقطة ما إذا كان حد الوظيفة عند نقطة معينة مساويًا لقيمة الدالة عند تلك النقطة:.

التعريف مفصل في وفقا للشروط:

1) يجب تحديد الوظيفة عند النقطة ، أي يجب أن تكون القيمة موجودة.

2) يجب أن يكون هناك حد مشترك للوظيفة. كما هو مذكور أعلاه ، هذا يعني وجود ومساواة حدود من جانب واحد: .

3) يجب أن يكون حد الوظيفة عند نقطة معينة مساويًا لقيمة الوظيفة في هذه المرحلة:.

إذا انتهكت مرة على الأقلمن ثلاثة شروط، ثم تفقد الوظيفة خاصية الاستمرارية عند النقطة.

استمرارية دالة في فترةتمت صياغته بطريقة ذكية وبسيطة للغاية: تكون الوظيفة متصلة على فترة زمنية إذا كانت متصلة في كل نقطة من الفترة الزمنية المحددة.

على وجه الخصوص ، العديد من الوظائف مستمرة في الفترة اللانهائية ، أي على مجموعة الأعداد الحقيقية. هذه دالة خطية ، كثيرات الحدود ، الأس ، الجيب ، جيب التمام ، إلخ. وبوجه عام ، أي دالة ابتدائيةمستمر على ذلك المجالات، على سبيل المثال، دالة لوغاريتميةمستمر على الفاصل الزمني. آمل أن تكون لديك الآن فكرة جيدة عما تبدو عليه الرسوم البيانية للوظائف الرئيسية. لمزيد من المعلومات حول استمراريتها ، انظر رجل صالحاسمه Fichtenholtz.

مع استمرارية الوظيفة في المقطع ونصف الفواصل الزمنية ، كل شيء بسيط أيضًا ، لكن من الأنسب التحدث عن هذا في الدرس على إيجاد القيم الدنيا والقصوى لدالة ما على قطعةحتى ذلك الحين ، دعونا نحافظ على رؤوسنا منخفضة.

تصنيف نقاط الانكسار

الحياة الرائعة للوظائف غنية بجميع أنواع النقاط الخاصة ، ونقاط الانهيار ليست سوى واحدة من صفحات سيرتهم الذاتية.

ملحوظة : فقط في حالة ، سوف أتطرق إلى لحظة أولية: نقطة الانهيار هي دائمًا نقطة واحدة- لا توجد "عدة نقاط فاصل متتالية" ، أي أنه لا يوجد شيء مثل "فاصل فاصل".

وتنقسم هذه النقاط بدورها إلى مجموعتين كبيرتين: فواصل من النوع الأولو فواصل من النوع الثاني. كل نوع من الاستراحة له خاصته صفاتالذي سننظر إليه الآن:

نقطة الانقطاع من النوع الأول

إذا تم انتهاك شرط الاستمرارية عند نقطة ما وحدود أحادية الجانب محدود ، ثم يطلق عليه نقطة الانهيار من النوع الأول.

لنبدأ بالحالة الأكثر تفاؤلاً. وفقًا للفكرة الأولية للدرس ، أردت أن أخبر النظرية "في نظرة عامة"، ولكن لإثبات حقيقة المادة ، فقد استقر على متغير مع جهات فاعلة محددة.

للأسف ، مثل صورة للعروسين في الخلفية شعلة أزلية، ولكن الإطار التالي مقبول بشكل عام. لنرسم رسمًا بيانيًا للوظيفة في الرسم:


هذه الوظيفة متصلة على خط الأعداد بالكامل ، باستثناء النقطة. في الواقع ، لا يمكن أن يكون المقام مساويًا للصفر. ومع ذلك ، وفقا لمعنى الحد - نستطيع قريب بلا حدودتقترب من "الصفر" من اليسار ومن اليمين ، أي أن الحدود أحادية الجانب موجودة ، ومن الواضح أنها تتطابق:
(تم استيفاء شرط الاستمرارية رقم 2).

لكن لم يتم تحديد الوظيفة عند هذه النقطة ، وبالتالي ، يتم انتهاك الشرط رقم 1 من الاستمرارية ، وتعاني الوظيفة من انقطاع في هذه المرحلة.

كسر من هذا النوع (مع القائمة حد عام) وتسمى فجوة قابلة للإصلاح. لماذا قابلة للإزالة؟ لأن الوظيفة يمكن إعادة تعريفعند نقطة الانهيار:

هل يبدو غريبا؟ ربما. لكن مثل هذا السجل الوظيفي لا يتعارض مع أي شيء! الآن تم إصلاح الفجوة والجميع سعداء:


لنقم بفحص رسمي:

2) - هناك حد مشترك ؛
3)

وبالتالي ، يتم استيفاء جميع الشروط الثلاثة ، وتكون الوظيفة متصلة عند نقطة من خلال تعريف استمرارية الوظيفة عند نقطة ما.

ومع ذلك ، يمكن لكارهي ماتان إعادة تعريف الوظيفة بطريقة سيئة ، على سبيل المثال :


من الغريب أن أول شرطين من شروط الاستمرارية مستوفيان هنا:
1) - يتم تحديد الوظيفة في نقطة معينة ؛
2) - هناك حد مشترك.

لكن الحد الثالث لم يتم تجاوزه: أي حد الوظيفة عند هذه النقطة غير متساويقيمة الوظيفة المعينة عند نقطة معينة.

وهكذا ، عند نقطة ما ، تعاني الوظيفة من انقطاع.

الحالة الثانية الأكثر حزناً تسمى كسر من النوع الأول بقفزة. والحزن هو الذي يثيره حدود من جانب واحد محدودة ومختلفة. يتم عرض مثال في الرسم الثاني للدرس. عادة ما تحدث هذه الفجوة في متعدد التعريف وظائفسبق ذكره في المقال. حول تحولات الرسم البياني.

ضع في اعتبارك دالة متعددة التعريف وتنفيذ الرسم لها. كيف تبني رسم بياني؟ بسيط جدا. في نصف الفاصل ، نرسم جزءًا من القطع المكافئ ( اللون الاخضر) ، في الفاصل الزمني - مقطع خط مستقيم (أحمر) وعلى نصف فاصل - خط مستقيم ( لون ازرق).

في الوقت نفسه ، بسبب عدم المساواة ، يتم تحديد القيمة وظيفة من الدرجة الثانية(النقطة الخضراء) ، وبسبب عدم المساواة ، يتم تحديد القيمة لوظيفة خطية (النقطة الزرقاء):

في أصعب الحالات ، يجب على المرء أن يلجأ إلى البناء النقطي لكل قطعة من الرسم البياني (انظر الأول درس حول الرسوم البيانية للوظائف).

في الوقت الحالي ، نحن مهتمون فقط بهذه النقطة. دعنا نفحصها من أجل الاستمرارية:

2) احسب الحدود من جانب واحد.

على اليسار لدينا قطعة ذات خط أحمر ، وبالتالي فإن الحد الأيسر هو:

على اليمين يوجد الخط الأزرق المستقيم ، والحد الأيمن:

نتيجة ل، أعداد محدودة، و هم غير متساوي. لأن حدود من جانب واحد محدودة ومختلفة: ، ثم تتأثر وظيفتنا انقطاع من النوع الأول مع قفزة.

من المنطقي أنه لا يمكن القضاء على الفجوة - لا يمكن حقًا تعريف الوظيفة بشكل أكبر و "عدم لصقها معًا" ، كما في المثال السابق.

نقاط الانقطاع من النوع الثاني

عادة ، تُنسب جميع حالات التمزق الأخرى بشكل مكر إلى هذه الفئة. لن أسرد كل شيء ، لأنك ستواجه عمليًا في 99٪ من المهام فجوة لا نهاية لها- عند استخدام اليد اليسرى أو اليمنى ، وفي كثير من الأحيان ، يكون كلا الحدين غير محدود.

وبالطبع ، فإن الصورة الأكثر وضوحًا هي المبالغة عند الصفر. هنا كلا الحدين من جانب واحد لانهائي: لذلك ، فإن الوظيفة تعاني من انقطاع من النوع الثاني عند النقطة.

أحاول ملء مقالاتي بالمحتوى الأكثر تنوعًا ، لذلك دعونا نلقي نظرة على الرسم البياني للوظيفة ، والذي لم يتم رؤيته بعد:

وفقًا للمخطط القياسي:

1) لم يتم تعريف الوظيفة في هذه المرحلة لأن المقام يذهب إلى الصفر.

بالطبع ، يمكن للمرء أن يستنتج على الفور أن الوظيفة تعاني من انقطاع عند النقطة ، ولكن سيكون من الجيد تصنيف طبيعة الفاصل ، والذي غالبًا ما يتطلبه الشرط. لهذا:

أذكرك أن التسجيل يعني عدد سالب متناهي الصغر، وتحت الدخول - عدد موجب متناهي الصغر.

الحدود من جانب واحد لانهائية ، مما يعني أن الوظيفة تعاني من انقطاع من النوع الثاني عند النقطة. المحور ص هو الخط المقارب الرأسيللرسم البياني.

ليس من النادر وجود كلتا الحدين من جانب واحد ، لكن أحدهما فقط لانهائي ، على سبيل المثال:

هذا هو الرسم البياني للدالة.

ندرس نقطة الاستمرارية:

1) الوظيفة غير محددة في هذه المرحلة.

2) احسب الحدود من جانب واحد: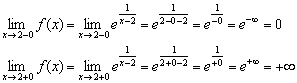

سنتحدث عن منهجية حساب هذه الحدود من جانب واحد في المثالين الأخيرين من المحاضرة ، على الرغم من أن العديد من القراء قد رأوا بالفعل وخمنوا كل شيء.

الحد الأيسر منتهي ويساوي صفرًا ("لا نذهب إلى النقطة نفسها") ، لكن الحد الأيمن غير محدود فرع البرتقالالرسومات قريبة بشكل لا نهائي من رسوماتهم الخط المقارب الرأسيتعطى بالمعادلة (الخط الأسود المتقطع).

وبالتالي ، فإن الوظيفة تعاني كسر من النوع الثانيعند نقطة .

بالنسبة للانقطاع من النوع الأول ، يمكن تحديد وظيفة عند نقطة الانقطاع نفسها. على سبيل المثال ، لدالة متعددة التعريف ضع نقطة سوداء جريئة في الأصل بجرأة. يوجد على اليمين فرع من القطع الزائد ، والنهاية اليمنى لا نهائية. أعتقد أن الجميع تقريبًا تخيل كيف يبدو هذا الرسم البياني.

ما كان يتطلع إليه الجميع:

كيف تتحقق من دالة للاستمرارية؟

يتم إجراء دراسة وظيفة الاستمرارية عند نقطة ما وفقًا للمخطط الروتيني الذي تم تدويره بالفعل ، والذي يتكون من التحقق من ثلاثة شروط للاستمرارية:

مثال 1

اكتشف الوظيفة

حل:

1) تقع النقطة الوحيدة تحت الأنظار ، حيث لا يتم تحديد الوظيفة.

2) احسب الحدود من جانب واحد:

الحدود من جانب واحد محدودة ومتساوية.

وهكذا ، عند نقطة ما ، تعاني الوظيفة من انقطاع مستمر.

كيف يبدو الرسم البياني لهذه الوظيفة؟

أريد التبسيط ، ويبدو أنه قطع مكافئ عادي. لكنلم يتم تحديد الوظيفة الأصلية عند هذه النقطة ، لذا فإن التحذير التالي مطلوب:

لننفذ الرسم:

إجابة: الوظيفة متصلة على خط الأعداد بالكامل باستثناء النقطة التي تعاني فيها من انقطاع.

يمكن إعادة تعريف الوظيفة بطريقة جيدة أو غير جيدة ، ولكن هذا ليس مطلوبًا من قبل الشرط.

تقول أن المثال بعيد المنال؟ مُطْلَقاً. حدث عشرات المرات في الممارسة. تأتي جميع مهام الموقع تقريبًا من عمل مستقل حقيقي وتحكمي.

دعنا نقسم الوحدات المفضلة لدينا:

مثال 2

اكتشف الوظيفة من أجل الاستمرارية. تحديد طبيعة فواصل الوظيفة ، إن وجدت. تنفيذ الرسم.

حل: لسبب ما ، يخاف الطلاب ولا يحبون الوظائف التي تحتوي على وحدة ، على الرغم من عدم وجود شيء معقد فيها. لقد تطرقنا بالفعل إلى مثل هذه الأشياء قليلاً في الدرس. تحولات الرسم الهندسي. نظرًا لأن المعامل غير سالب ، فإنه يتمدد على النحو التالي: ، حيث "alpha" عبارة عن بعض التعبيرات. في هذه الحالة ، يجب أن تشير وظيفتنا متعددة التعريف:

لكن كسور كلتا القطعتين يجب أن تُختزل بمقدار. التخفيض ، كما في المثال السابق ، لن يمر دون عواقب. لم يتم تعريف الوظيفة الأصلية عند النقطة لأن المقام يتلاشى. لذلك ، يجب على النظام تحديد الشرط بالإضافة إلى ذلك ، وجعل المتباينة الأولى صارمة:

الآن من أجل خدعة مفيدة للغاية: قبل الانتهاء من المهمة في المسودة ، من المفيد عمل رسم (بغض النظر عما إذا كان الشرط مطلوبًا أم لا). سيساعد هذا ، أولاً ، على رؤية نقاط الاستمرارية ونقاط الانقطاع على الفور ، وثانيًا ، سيوفر لك 100٪ من الأخطاء عند العثور على حدود من جانب واحد.

لنفعل الحيلة. وفقًا لحساباتنا ، على يسار النقطة ، من الضروري رسم جزء من القطع المكافئ (الأزرق) ، وإلى اليمين - قطعة من القطع المكافئ (الأحمر) ، بينما لم يتم تحديد الوظيفة عند النقطة نفسها :

عندما تكون في شك ، خذ بعض قيم "x" ، واستبدلها في الدالة (تذكر أن الوحدة تدمر علامة ناقص محتملة) وتحقق من الرسم البياني.

نحن نحقق في وظيفة الاستمرارية تحليليًا:

1) لم يتم تحديد الوظيفة عند هذه النقطة ، لذلك يمكننا القول على الفور أنها ليست متصلة بها.

2) دعونا نحدد طبيعة الانقطاع ، ولهذا نحسب الحدود من جانب واحد:

الحدود أحادية الجانب محدودة ومختلفة ، مما يعني أن الوظيفة تعاني من انقطاع من النوع الأول مع قفزة عند النقطة. مرة أخرى ، لاحظ أنه عند إيجاد الحدود ، لا يهم ما إذا كانت الوظيفة عند نقطة الفاصل محددة أم لا.

يبقى الآن نقل الرسم من المسودة (تم إجراؤه ، كما كان ، بمساعدة البحث ؛-)) وإكمال المهمة:

إجابة: الوظيفة متصلة على خط الأعداد بالكامل باستثناء النقطة التي تعاني فيها من انقطاع من النوع الأول مع قفزة.

في بعض الأحيان يكون مطلوبًا الإشارة بشكل إضافي إلى قفزة التوقف. يتم حسابها بشكل أساسي - يجب طرح الحد الأيسر من الحد الأيمن: أي عند نقطة الانقطاع ، قفزت وظيفتنا بمقدار وحدتين إلى الأسفل (وهو ما تخبرنا به علامة الطرح).

مثال 3

اكتشف الوظيفة من أجل الاستمرارية. تحديد طبيعة فواصل الوظيفة ، إن وجدت. جعل الرسم.

هذا مثال على حل مستقل, عينة نموذجيةالحلول في نهاية الدرس.

دعنا ننتقل إلى الإصدار الأكثر شيوعًا والأكثر شيوعًا للمهمة ، عندما تتكون الوظيفة من ثلاث أجزاء:

مثال 4

تحقق من دالة الاستمرارية وارسم الرسم البياني للوظيفة .

حل: من الواضح أن جميع الأجزاء الثلاثة للدالة متصلة على الفترات المقابلة ، لذلك يبقى التحقق من نقطتي "تقاطع" فقط بين القطع. أولاً ، دعنا نرسم مسودة ، لقد علقت على تقنية البناء بتفاصيل كافية في الجزء الأول من المقالة. الشيء الوحيد هو اتباع النقاط الفردية بعناية: نظرًا لعدم المساواة ، تنتمي القيمة إلى الخط المستقيم (النقطة الخضراء) ، وبسبب عدم المساواة ، تنتمي القيمة إلى القطع المكافئ (النقطة الحمراء):


حسنًا ، من حيث المبدأ ، كل شيء واضح =) يبقى اتخاذ قرار. لكل من النقطتين "بعقب" ، نتحقق من 3 شروط للاستمرارية كمعيار:

أنا)ندرس نقطة الاستمرارية

1)

الحدود أحادية الجانب محدودة ومختلفة ، مما يعني أن الوظيفة تعاني من انقطاع من النوع الأول مع قفزة عند النقطة.

دعونا نحسب قفزة التوقف على أنها الفرق بين الحدين الأيمن والأيسر:
، أي أن المخطط قفز بمقدار وحدة واحدة.

II)ندرس نقطة الاستمرارية

1) - يتم تحديد الوظيفة عند نقطة معينة.

2) ابحث عن حدود من جانب واحد:

- الحدود أحادية الجانب محدودة ومتساوية ، لذلك هناك حد مشترك.

3) - حدود دالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

في المرحلة النهائية ، ننقل الرسم إلى نسخة نظيفة ، وبعد ذلك نضع الوتر النهائي:

إجابة: الوظيفة متصلة على خط الأعداد بالكامل ، باستثناء النقطة التي تعاني فيها من انقطاع من النوع الأول مع قفزة.

مثال 5

تحقق من دالة للاستمرارية وقم ببناء الرسم البياني الخاص بها .

هذا مثال لحل مستقل ، حل قصير وعينة تقريبية للمشكلة في نهاية الدرس.

قد يكون لدى المرء انطباع بأنه في مرحلة ما يجب بالضرورة أن تكون الوظيفة مستمرة ، وفي نقطة أخرى يجب بالضرورة أن يكون هناك انقطاع. في الممارسة العملية ، هذا ليس هو الحال دائمًا. حاول ألا تهمل الأمثلة المتبقية - سيكون هناك العديد من الميزات المثيرة للاهتمام والمهمة:

مثال 6

إعطاء وظيفة . تحقق من وظيفة الاستمرارية عند النقاط. أنشئ رسمًا بيانيًا.

حل: ومرة ​​أخرى نفّذ الرسم على المسودة فورًا:

خصوصية هذا الرسم البياني هي أنه بالنسبة للدالة متعددة التعريف ، يتم الحصول عليها من خلال معادلة محور الإحداثي. هنا هذا الموقعتتبع بالأخضر، وعادة ما يتم تمييزه في دفتر ملاحظات بخط عريض بقلم رصاص بسيط. وبالطبع ، لا تنسوا خرافنا: تشير القيمة إلى فرع الظل (النقطة الحمراء) ، والقيمة تنتمي إلى الخط المستقيم.

كل شيء واضح من الرسم - الوظيفة مستمرة على خط الأرقام بالكامل ، ويبقى وضع حل يتم إحضاره إلى الأتمتة الكاملة حرفيًا بعد 3-4 أمثلة مماثلة:

أنا)ندرس نقطة الاستمرارية

1) - يتم تحديد الوظيفة عند نقطة معينة.

2) احسب الحدود من جانب واحد:

، لذلك هناك حد مشترك.

فقط لكل رجل إطفاء ، دعني أذكرك بحقيقة تافهة: حد الثابت يساوي الثابت نفسه. في هذه الحالة ، نهاية الصفر تساوي صفرًا نفسها (النهاية اليسرى).

3) - حدود دالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

وبالتالي ، تكون الوظيفة متصلة عند نقطة ما بتعريف الدالة المستمرة عند نقطة ما.

II)ندرس نقطة الاستمرارية

1) - يتم تحديد الوظيفة عند نقطة معينة.

2) ابحث عن حدود من جانب واحد:

وهنا - حد الوحدة يساوي الوحدة نفسها.

- هناك حد مشترك.

3) - حدود دالة عند نقطة ما تساوي قيمة هذه الدالة عند نقطة معينة.

وبالتالي ، تكون الوظيفة متصلة عند نقطة ما بتعريف الدالة المستمرة عند نقطة ما.

كالعادة ، بعد الدراسة ، ننقل رسمنا إلى نسخة نظيفة.

إجابة: الوظيفة مستمرة عند النقاط.

يرجى ملاحظة أنه في حالة عدم سؤالنا عن أي شيء عن دراسة الوظيفة بأكملها من أجل الاستمرارية ، وتعتبر صيغة رياضية جيدة للصياغة دقيق وواضحالإجابة على السؤال المطروح. بالمناسبة ، إذا كان الشرط غير مطلوب لإنشاء رسم بياني ، فعندئذ يكون لديك حق كامللا تقم ببنائها (على الرغم من أن المعلم قد يجبرها لاحقًا على القيام بذلك).

"طقطقة" رياضية صغيرة لحل مستقل:

مثال 7

إعطاء وظيفة . تحقق من وظيفة الاستمرارية عند النقاط. تصنيف نقاط التوقف ، إن وجدت. تنفيذ الرسم.

حاول "نطق" كل "الكلمات" بشكل صحيح =) وارسم الرسم البياني بدقة أكبر ، لن يكون الأمر غير ضروري في كل مكان ؛-)

كما تتذكر ، أوصيت بأن ترسم على الفور مسودة ، ولكن من وقت لآخر توجد أمثلة لا يمكنك فيها على الفور معرفة شكل الرسم البياني. لذلك ، في عدد من الحالات ، من المفيد أولاً العثور على حدود من جانب واحد وبعد ذلك فقط ، بناءً على الدراسة ، تصور الفروع. في المثالين الأخيرين ، سنتعلم أيضًا تقنية حساب بعض الحدود من جانب واحد:

المثال 8

تحقق من دالة للاستمرارية وقم ببناء الرسم البياني التخطيطي الخاص بها.

حل: النقاط السيئة واضحة: (يحول مقام الأس إلى الصفر) و (يتحول إلى الصفر في مقام الكسر بأكمله). ليس من الواضح كيف يبدو الرسم البياني لهذه الوظيفة ، مما يعني أنه من الأفضل إجراء البحث أولاً.

ضع في اعتبارك وظيفتين تظهر الرسوم البيانية في الشكل. 1 و 2. يمكن رسم الرسم البياني للوظيفة الأولى بدون رفع القلم الرصاص عن الورقة. هذه الوظيفة يمكن أن تسمى مستمرة. من المستحيل رسم رسم بياني لوظيفة أخرى بهذه الطريقة. يتكون من قطعتين متصلتين ، وعند نقطة ما يكون له انقطاع ، وسوف نسمي الدالة غير متصلة.

مثل هذا التعريف المرئي للاستمرارية لا يمكن أن يناسب الرياضيات بأي شكل من الأشكال ، لأنه يحتوي على مفاهيم غير رياضية تمامًا مثل "قلم رصاص" و "ورقة". يتم تقديم التعريف الرياضي الدقيق للاستمرارية على أساس مفهوم الحد ويتكون مما يلي.

دع وظيفة يتم تعريفها على مقطع وتكون نقطة ما في هذا المقطع. تسمى الوظيفة مستمرة عند نقطة ما إذا كانت قيم الوظيفة تميل إلى ، كما تميل (يتم اعتبارها من جزء فقط) ، أي لو

. (1)

تسمى الوظيفة متصلة على مقطع ما إذا كانت متصلة عند كل نقطة عليها.

إذا لم يتم استيفاء المساواة (1) عند هذه النقطة ، فإن الوظيفة تسمى متقطعة عند النقطة.

كما نرى ، رياضيًا يتم تحديد خاصية الاستمرارية لوظيفة ما على مقطع ما من خلال خاصية الاستمرارية المحلية (المحلية) عند نقطة ما.

تسمى القيمة زيادة الوسيطة ، ويسمى الفرق بين قيم الوظيفة زيادة الدالة ويتم الإشارة إليها بواسطة. من الواضح ، عندما تميل إلى الزيادة في الوسيطة تميل إلى الصفر:.

دعونا نعيد كتابة المساواة (1) بالشكل المكافئ

.

باستخدام الترميز المقدم ، يمكن إعادة كتابته على النحو التالي:

لذلك ، إذا كانت الدالة متصلة ، فعندما تميل زيادة الوسيطة إلى الصفر ، فإن زيادة الدالة تميل إلى الصفر. يقولون خلاف ذلك: زيادة صغيرة في الوسيطة تتوافق مع زيادة صغيرة في الوظيفة. على التين. يوضح الشكل 3 رسمًا بيانيًا لوظيفة متصلة عند نقطة ما ، وتتوافق الزيادة مع زيادة الدالة. على التين. 4 زيادة تقابل مثل هذه الزيادة في الوظيفة ، والتي ، مهما كانت صغيرة ، لن تقل عن نصف طول المقطع ؛ الوظيفة غير متصلة عند النقطة.

إن فكرتنا عن وظيفة مستمرة كدالة يمكن رسم رسم بياني لها دون رفع القلم الرصاص عن الورقة مدعومة تمامًا بخصائص الوظائف المستمرة التي تم إثباتها في حساب التفاضل والتكامل. دعونا نلاحظ ، على سبيل المثال ، خصائصهم.

1. إذا كانت دالة متصلة في مقطع ما تأخذ قيمًا لعلامات مختلفة في نهايات المقطع ، فإنها تأخذ قيمة تساوي صفرًا في نقطة ما من هذا المقطع.

2. تأخذ الوظيفة ، المستمرة على المقطع ، جميع القيم الوسيطة بين القيم عند نقاط النهاية ، أي بين و .

3. إذا كانت الدالة متصلة على مقطع ما ، فإنها تصل في هذا المقطع إلى الحد الأقصى لها والدالة الخاصة بها أصغر قيمة، أي. إذا - أصغر ، و - أكبر قيم للدالة في المقطع ، فهناك نقاط على هذا المقطع و ، كذا ، و.

المعنى الهندسي لأول هذه العبارات واضح تمامًا: إذا مر منحنى مستمر من جانب واحد من المحور إلى الآخر ، فإنه يتقاطع مع هذا المحور (الشكل 5). لا تحتوي الوظيفة غير المستمرة على هذه الخاصية ، والتي أكدها الرسم البياني للوظيفة في الشكل. 2 ، فضلا عن الخصائص 2 و 3. في التين. 2 لا تأخذ القيمة ، على الرغم من أنها محاطة بين و. على التين. يُظهر الشكل 6 مثالاً على دالة غير متصلة (الجزء الكسري من الرقم) لا تصل إلى قيمتها القصوى ..

يؤدي الجمع والطرح وضرب الدوال المستمرة على نفس المقطع مرة أخرى إلى وظائف مستمرة. عند قسمة وظيفتين مستمرتين ، يتم الحصول على دالة متصلة إذا كان المقام مختلفًا عن الصفر في كل مكان.

توصلت الرياضيات إلى مفهوم الوظيفة المستمرة من خلال دراسة قوانين الحركة المختلفة ، أولاً وقبل كل شيء. المكان والزمان مستمران ، ويعطي اعتماد المسار على الوقت ، على سبيل المثال ، الذي يعبر عنه القانون ، مثالاً على وظيفة مستمرة.

تصف الوظائف المستمرة الحالات والعمليات في المواد الصلبة والسوائل والغازات. تتحد العلوم التي تدرسها - نظرية المرونة والديناميكا المائية والديناميكا الهوائية - باسم واحد - "ميكانيكا الاتصال".

في هذا الدرس ، سوف نتعلم كيفية إنشاء استمرارية دالة. سنفعل ذلك بمساعدة الحدود ، علاوة على ذلك ، من جانب واحد - يمينًا ويسارًا ، وهي ليست مخيفة على الإطلاق ، على الرغم من حقيقة أنها مكتوبة بصيغة و.

ولكن ما هي استمرارية الوظيفة بشكل عام؟ حتى نصل إلى تعريف دقيق ، أسهل طريقة لتخيل خط يمكن رسمه دون رفع القلم الرصاص عن الورقة. إذا تم رسم هذا الخط ، فهو مستمر. هذا الخط هو الرسم البياني لوظيفة مستمرة.

بيانياً ، تكون الوظيفة متصلة عند نقطة ما إذا لم "ينكسر" رسمها البياني عند تلك النقطة. الرسم البياني لمثل هذه الوظيفة المستمرة هو هو مبين في الشكل أدناه.

تعريف استمرارية الدالة حتى النهاية.الدالة مستمرة عند نقطة تحت ثلاثة شروط:

1. يتم تحديد الوظيفة عند هذه النقطة.

إذا لم يتم استيفاء شرط واحد على الأقل من الشروط المذكورة أعلاه ، فإن الوظيفة ليست متصلة عند نقطة ما. في الوقت نفسه ، يقولون إن الوظيفة تعاني من انقطاع ، والنقاط على الرسم البياني التي يتم فيها مقاطعة الرسم البياني تسمى نقاط فاصل الدالة. يظهر الرسم البياني لمثل هذه الوظيفة ، والذي يعاني من انقطاع عند النقطة x = 2 ، في الشكل أدناه.

مثال 1وظيفة F(x) على النحو التالي:

هل ستكون هذه الوظيفة مستمرة عند كل نقطة من نقاط حدود فروعها ، أي عند النقاط x = 0 , x = 1 , x = 3 ?

حل. نتحقق من الشروط الثلاثة لاستمرارية الوظيفة عند كل نقطة حدية. تم استيفاء الشرط الأول بسبب وظيفة محددةفي كل نقطة من النقاط الحدودية يتبع من تعريف الوظيفة. يبقى التحقق من الشرطين المتبقيين.

نقطة x= 0. أوجد النهاية اليسرى عند هذه النقطة:

.

لنجد حد اليد اليمنى:

x= 0 يجب العثور عليها في فرع الوظيفة الذي يتضمن هذه النقطة ، أي الفرع الثاني. نجدهم:

كما ترى ، حد الوظيفة وقيمة الدالة عند النقطة x= 0 متساوون. لذلك ، فإن الوظيفة متصلة عند النقطة x = 0 .

نقطة x= 1. أوجد النهاية اليسرى عند هذه النقطة:

لنجد حد اليد اليمنى:

حد الوظيفة وقيمة الوظيفة عند نقطة x= 1 يجب العثور عليها في فرع الوظيفة الذي يتضمن هذه النقطة ، أي الفرع الثاني. نجدهم:

.

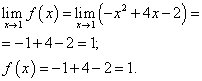حد الوظيفة وقيمة الوظيفة عند نقطة x= 1 متساوون. لذلك ، فإن الوظيفة متصلة عند النقطة x = 1 .

نقطة x= 3. أوجد النهاية اليسرى عند هذه النقطة:

لنجد حد اليد اليمنى:

حد الوظيفة وقيمة الوظيفة عند نقطة x= 3 يجب العثور عليها في فرع الوظيفة الذي يتضمن هذه النقطة ، أي الفرع الثاني. نجدهم:

.

حد الوظيفة وقيمة الوظيفة عند نقطة x= 3 متساوون. لذلك ، فإن الوظيفة متصلة عند النقطة x = 3 .

الاستنتاج الرئيسي: هذه الوظيفة مستمرة عند كل نقطة حدية.

حدد استمرارية دالة في نقطة ما بنفسك ، ثم انظر إلى الحل

يمكن تعريف التغيير المستمر في دالة على أنه تغيير تدريجي ، بدون قفزات ، يستلزم فيه تغيير بسيط في الوسيطة تغييرًا بسيطًا في الوظيفة.

دعنا نوضح هذا التغيير المستمر في الوظيفة بمثال.

دع الحمل معلقًا على خيط فوق الطاولة. تحت تأثير هذا الحمل ، يتم شد الخيط ، وبالتالي المسافة لالحمل من نقطة تعليق الخيط هو دالة لكتلة الحمل م، إنه ل = F(م) , م≥0 .

إذا قمنا بتغيير كتلة الحمل قليلاً ، ثم المسافة لتغيير طفيف: تغيير طفيف متتوافق مع التغييرات الصغيرة ل. ومع ذلك ، إذا كانت كتلة الحمل قريبة من قوة شد الخيط ، فإن الزيادة الطفيفة في كتلة الحمل يمكن أن تتسبب في كسر الخيط: المسافة لستزداد فجأة وتصبح مساوية للمسافة من نقطة التعليق إلى سطح الطاولة. رسم بياني وظيفي ل = F(م) هو مبين في الشكل. على الموقع ، هذا الرسم البياني عبارة عن خط متصل (متصل) ، وعند هذه النقطة يتم مقاطعته. والنتيجة هي رسم بياني يتكون من فرعين. في جميع النقاط ما عدا الوظيفة ل = F(م) هو مستمر ، وعند نقطة ما يكون لديه انقطاع.

يمكن أن تكون دراسة دالة من أجل الاستمرارية مهمة مستقلة وأحد مراحل دراسة كاملة للوظيفة وبناء الرسم البياني الخاص بها.

استمرارية دالة في فترة

دع الوظيفة ذ = F(x) المحددة في الفاصل الزمني] أ, ب[وهو مستمر في كل نقطة من هذه الفترة الزمنية. ثم يطلق عليه مستمر في الفترة الزمنية] أ, ب[. يتم تعريف مفهوم استمرارية الوظيفة على فترات من النموذج] - ∞ بشكل مشابه ، ب[ , ]أ، + ∞ [،] - ∞ ، + ∞ [. الآن دع الوظيفة ذ = F(x) المحددة في الفاصل الزمني [ أ, ب]. الفرق بين الفاصل الزمني والمقطع هو أن نقاط حدود الفاصل الزمني لم يتم تضمينها في الفاصل الزمني ، ولكن يتم تضمين نقاط حدود المقطع في المقطع. هنا يجب أن نذكر ما يسمى بالاستمرارية من جانب واحد: عند هذه النقطة أ، البقاء في الفاصل الزمني [ أ, ب] ، لا يمكننا الاقتراب إلا من اليمين وإلى النقطة ب- فقط على اليسار. تسمى الوظيفة مستمرة على المقطع [ أ, ب] ، إذا كان مستمرًا عند جميع النقاط الداخلية لهذا المقطع ، ومستمرًا على اليمين عند النقطة أويترك مستمرًا عند النقطة ب.

يمكن لأي من الوظائف الأولية أن تكون بمثابة مثال على وظيفة مستمرة. كل دالة ابتدائيةهو مستمر في أي جزء يتم تعريفه عليه. على سبيل المثال ، دوال ومتصلة على أي فترة [ أ, ب] ، الوظيفة مستمرة في المقطع [ 0 , ب] ، تكون الوظيفة متصلة على أي مقطع لا يحتوي على نقطة أ = 2 .

مثال 4تحقق من وظيفة الاستمرارية.

حل. دعنا نتحقق من الشرط الأول. لم يتم تحديد الوظيفة عند النقطتين - 3 و 3. لم يتم استيفاء شرط واحد على الأقل من الشروط لاستمرارية الوظيفة على خط الأرقام بالكامل. لذلك ، هذه الوظيفة مستمرة على الفترات

.

مثال 5تحديد قيمة المعلمة أمستمر طوال الوقت المجالاتوظيفة

حل.

لنجد حد اليد اليمنى لـ:

.

من الواضح أن القيمة عند هذه النقطة x= 2 يجب أن تكون متساوية فأس :

أ = 1,5 .

مثال 6تحديد قيم المعلمات أو بمستمر طوال الوقت المجالاتوظيفة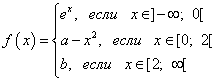

حل.
أوجد النهاية اليسرى للدالة عند النقطة:

.

لذلك ، يجب أن تكون القيمة عند النقطة مساوية لـ 1:

لنجد دالة الجانب الأيسر عند النقطة:

من الواضح أن قيمة الوظيفة عند النقطة يجب أن تكون مساوية لـ:

الإجابة: الوظيفة مستمرة على كامل مجال تعريف أ = 1; ب = -3 .

الخصائص الأساسية للوظائف المستمرة

توصلت الرياضيات إلى مفهوم الوظيفة المستمرة من خلال دراسة قوانين الحركة المختلفة ، أولاً وقبل كل شيء. المكان والزمان لا حصر لهما والتبعية مثل المسارات سمن وقت رالتي يعبر عنها القانون س = F(ر) ، يعطي مثالا على المستمر المهام F(ر). تتغير درجة حرارة الماء الساخن أيضًا بشكل مستمر ، وهي أيضًا وظيفة مستمرة للوقت: تي = F(ر) .

في التحليل الرياضي ، تم إثبات بعض خصائص الوظائف المستمرة. نقدم أهم هذه الخصائص.

1. إذا كانت دالة متصلة في فترة تأخذ قيمًا من علامات مختلفة في نهايات الفترة ، فإنها تأخذ قيمة تساوي صفرًا في نقطة ما من هذا المقطع. بشكل أكثر رسمية ، يتم إعطاء هذه الخاصية في نظرية تُعرف باسم نظرية بولزانو كوشي الأولى.

2. الوظيفة F(x) ، مستمر على الفاصل الزمني [ أ, ب] ، يأخذ جميع القيم الوسيطة بين القيم عند نقاط النهاية ، أي بين F(أ) و F(ب). بشكل أكثر رسمية ، يتم إعطاء هذه الخاصية في نظرية تُعرف باسم نظرية بولزانو كوشي الثانية.

وظيفة مستمرةهي وظيفة بدون "قفزات" ، أي وظيفة يتم استيفاء الشرط لها: التغييرات الصغيرة في الوسيطة تليها تغييرات صغيرة في القيم المقابلة للدالة. الرسم البياني لمثل هذه الوظيفة هو منحنى سلس أو مستمر.

يمكن تعريف الاستمرارية عند نقطة حد لمجموعة معينة باستخدام مفهوم الحد ، أي: يجب أن يكون للوظيفة حد عند هذه النقطة يساوي قيمتها عند نقطة النهاية.

إذا تم انتهاك هذه الشروط في مرحلة ما ، يُقال أن الوظيفة غير متصلة في هذه المرحلة ، أي أن استمراريتها مكسورة. في لغة الحدود ، يمكن وصف نقطة الانكسار بأنها عدم تطابق بين قيمة دالة عند نقطة فاصل وحد الوظيفة (إن وجدت).

يمكن أن تكون نقطة الفاصل قابلة للإزالة ؛ وهذا يتطلب وجود حد للوظيفة ، ولكن لا يتطابق مع قيمتها في نقطة معينة. في هذه الحالة ، يمكن "تصحيحه" في هذه المرحلة ، أي تمديده إلى الاستمرارية.
يتم تكوين صورة مختلفة تمامًا إذا كان حد الوظيفة في المعطى موجودًا. هناك نوعان من نقاط التوقف المحتملة:

• من النوع الأول - كلا الحدين من جانب واحد موجودان ومحدودان ، ولا تتطابق قيمة أحدهما أو كلاهما مع قيمة الوظيفة عند نقطة معينة ؛
• من النوع الثاني ، عندما لا يوجد أحد أو كلا الحدين الأحادي الجانب ، أو عندما تكون قيمهما غير محدودة.

خصائص الوظائف المستمرة

• الوظيفة التي تم الحصول عليها نتيجة العمليات الحسابية ، وكذلك تراكب الوظائف المستمرة في مجال تعريفها ، هي أيضًا مستمرة.
• بالنظر إلى دالة مستمرة تكون موجبة في مرحلة ما ، فمن الممكن دائمًا العثور على حي صغير بما يكفي للاحتفاظ بإشاراته.
• وبالمثل ، إذا كانت قيمه عند النقطتين A و B ، على التوالي ، a و b ، و a مختلفة عن b ، فعندئذٍ بالنسبة للنقاط الوسيطة ، سيأخذ جميع القيم من الفترة (أ ؛ ب). من هذا يمكننا استخلاص نتيجة مثيرة للاهتمام: إذا تركت الشريط المطاطي يتقلص بحيث لا يتدلى (يظل مستقيماً) ، فستظل إحدى نقاطه ثابتة. ومن الناحية الهندسية ، هذا يعني أن هناك خطًا يمر عبر أي نقطة وسيطة بين A و B ، والتي تتقاطع مع الرسم البياني للدالة.

نلاحظ بعض الوظائف الأولية المستمرة (في مجال تعريفها):

• ثابت؛
• عاقِل؛
• حساب المثاثات.

بين المفهومين الأساسيين في الرياضيات - الاستمرارية والتفاضل - هناك رابط لا ينفصل. يكفي أن نتذكر أنه لكي تكون الوظيفة قابلة للاشتقاق ، يجب أن تكون دالة مستمرة.

إذا كانت الوظيفة قابلة للاشتقاق في مرحلة ما ، فإنها تكون متصلة هناك. ومع ذلك ، ليس من الضروري على الإطلاق أن يكون مشتقها مستمرًا.

الوظيفة التي لها مشتق مستمر في مجموعة ما تنتمي إلى فئة منفصلة من الوظائف الملساء. بمعنى آخر ، إنها وظيفة قابلة للتفاضل باستمرار. إذا كان المشتق يحتوي على عدد محدود من نقاط عدم الاستمرارية (فقط من النوع الأول) ، فإن هذه الوظيفة تسمى سلسلة متجانسة.

مفهوم آخر مهم هو الاستمرارية المنتظمة للوظيفة ، أي قدرتها على أن تكون مستمرة على قدم المساواة في أي نقطة في مجال تعريفها. وبالتالي ، فهي خاصية يتم النظر فيها في مجموعة من النقاط ، وليس في أي واحد على وجه الخصوص.

إذا أصلحنا نقطة ، فلن نحصل على أكثر من تعريف للاستمرارية ، أي من وجود الاستمرارية المنتظمة يترتب على ذلك أن لدينا وظيفة مستمرة. بشكل عام ، العكس ليس صحيحًا. ومع ذلك ، وفقًا لنظرية كانتور ، إذا كانت الوظيفة مستمرة على مجموعة مضغوطة ، أي في فترة زمنية مغلقة ، فهي متصلة بشكل موحد عليها.